Refined Reheating
Numerically exploring the late very early universe
Quantum mechanics and gravity are famously irreconcilable, at least in their present forms. While this statement is prolific, the underlying reasons are fairly technical, primarily having to do with the rules for constructing quantum field theories. Worse still, the incredible weakness of gravity means that experimentally sifting through the plethora of elegant proposed solutions to the problem is exceedingly difficult. One of the precious few potentially probe-able areas of physics that should require the use of both theories is in the very early universe, during a period known as Inflation.
In the very beginning, there were giant question marks, but shortly following the epoch of punctuation we expect there was an epoch of wild exponential expansion. This period had to come to an end for us to exist today, so it needed to have been driven by a dynamic system (as opposed to a simple cosmological constant, which may be the leading contributor to universal expansion today). The most likely candidate for such a system would be a quantum field, and there lies the hope: a quantum field causing universe-sized gravitational effects must involve aspects of a quantum theory of gravity. Even this hypothetical phenomenon isn’t likely to involve a full theory of quantum gravity, but it involves enough of an overlap we should be able to at least start to poke at the full theory.
The inflationary period itself is relatively tractable analytically. The rapid exponential expansion of the universe essentially washes out all of the interesting diversity of local fluctuations, leaving a simplified system even a theoretical physicist can handle. Once the inflation itself comes to an end, the real fun begins. Inflation leaves a cold, flat, dead universe, but bit by bit, whatever little statistical fluctuations remained begin to grow, and eventually trigger the real non-linear complexity of the equations of motion. In a fully non-linear system chaos can ensue, individual momentum modes can become caught up in the fun and grow wildly out of proportion, dumping energy into the field (not from nowhere of course, extracted from the expansion of the universe). This period is known as reheating, and due to its wild, carefree nature, it is only really approachable numerically.
Of course numerical explorations of reheating are nothing new, but what is new is our use of refinement. The code we are writing to explore this regime and the wacky characters involved is a “smart” code, it can identify where interesting things are happening and increase the simulation’s resolution in only a small neighbourhood around them. This is numerically the best of both worlds; we’re trying to simulate the universe here, so we’re obviously expecting a huge portion of our simulation volume to be basically empty, but we still need to simulate it so the non-empty bits are free to fully explore their environment and interact with each other. For example, we may have a slice of the universe that looks like the following:
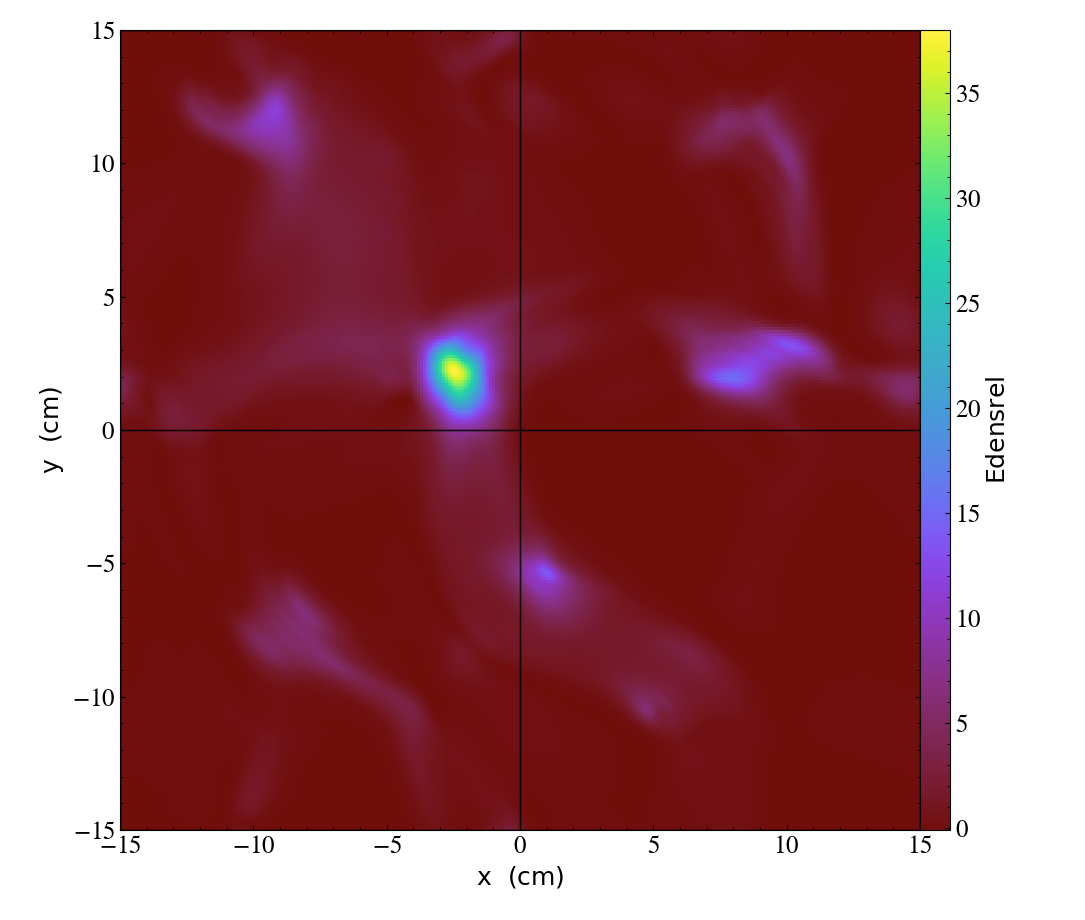
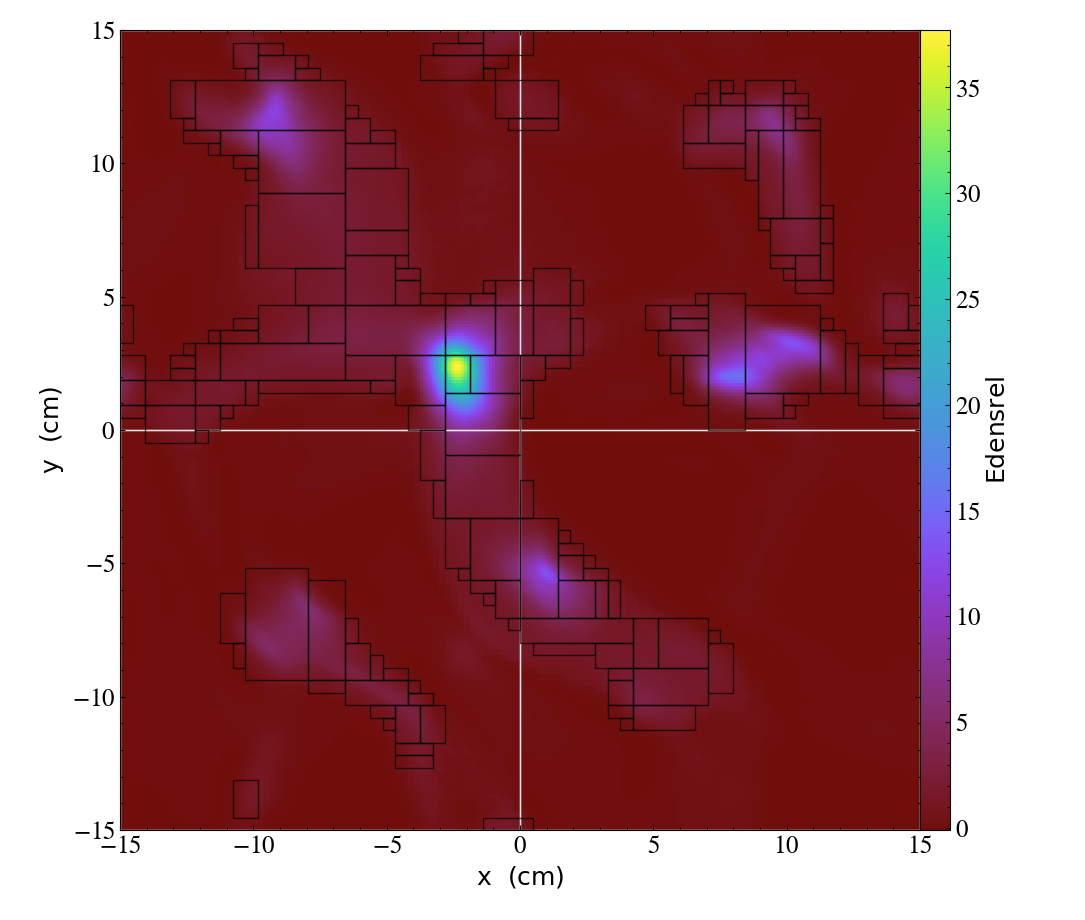
In the top slice we have spent a lot of computational effort to simulate the entire universe at the same fine resolution (\(256^3\)). In the bottom slice, we have a very coarse base resolution (\(128^3\)), but we increase it to match the fine resolution of the top simulation only in black grids. The second simulation ran much faster than the first, but clearly found the same dynamics.
There are still a lot of bugs to work out in the code at the moment, but as we progress we’ll be interested in a number of questions, such as the following.
Questions to ask:
- How does energy conservation work with bound states (oscillons) in the inflaton field? In practical terms, when (if at all) do these local structures stop feeling the expansion of the universe?
- Oscillons are big clumps of matter, they should generate a gravitational field and feel the pull of their neighbours! What do the dynamics and resulting power spectrum look like if we include local gravity?
- Oscillons are just one of the non-linear features of the inflaton field's solution space! Another well-known example are the topological solitons; what happens to the gravitational wave spectrum of the early universe when we include both of these creatures in the dynamics?